Distributome Colorblindness Activity
Overview
Colorblindness – Can you see the number in this image? 
This Distributome Activity illustrates an application of probability theory to study Colorblindness, typically a genetic disorder which results from an abnormality on the X chromosome. The condition is thus rarer in women since a woman would need to have the abnormality on both of her X chromosomes in order to be colorblind (whether a woman has the abnormality on one X chromosome is essentially independent of having it on the other).
Goals
The goal of this activity is to demonstrate an efficient protocol of estimating the probability that a randomly chosen individual may be colorblind.
Hands-on Activity
Suppose that \(p\) is the probability that a randomly selected ”man” is colorblind.
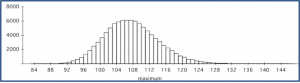
- 100 men are selected at random. What is the distribution of \(X_m\) = the number of these men that are colorblind?
- 100 women are selected at random. What is the distribution of \(X_f\) = the number of these women that are colorblind?
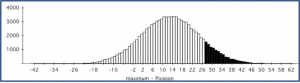
- To estimate the probability that a randomly selected woman is colorblind, you might use the proportion of colorblind women in a sample of n women. What is the variance of this estimator?
- Alternatively, to estimate the probability that a randomly selected woman is colorblind, you might use the square of the proportion of colorblind men in a sample of n men. Explain why this estimate makes sense. What is the variance of this estimator?
- For large samples, is it better to use a sample of men or a sample of women to estimate the probability that a randomly selected women is colorblind? Explain.
Alternate approach
You can also use the delta method to find the approximate variance for the estimator above.
Conclusions
In practice, it may difficult to obtain reliable parameter estimates when the event at hand is very rare (such as with colorblindness in women). The use of a valid probability model such as the relationship between the chance of colorblindness in men and the chance in women may improve these estimates.